Prev Next

Water Tank Pressure Regulator

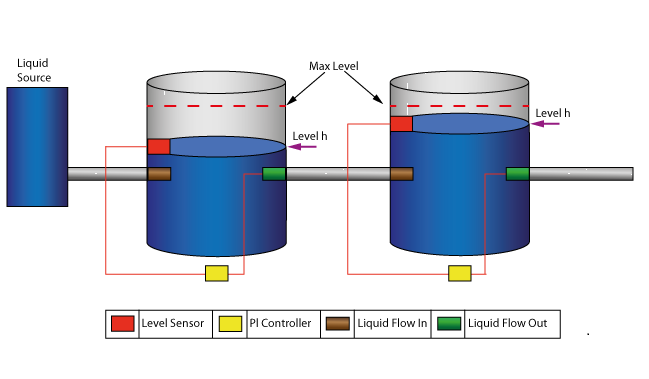
In this section we will walk through the creation of a SysML parametric model for a Water Tank Pressure Regulator, composed of two connected tanks, a source of water and two controllers, each of which monitors the water level and controls the valve to regulate the system.

We will explain the SysML model, create it and set up the SysMLSim Configurations. We will then run the simulation with OpenModelica.

System being modeled

This diagram depicts two tanks connected together, and a water source that fills the first tank. Each tank has a proportional–integral (PI) continuous controller connected to it, which regulates the level of water contained in the tanks at a reference level. While the source fills the first tank with water the PI continuous controller regulates the outflow from the tank depending on its actual level. Water from the first tank flows into the second tank, which the PI continuous controller also tries to regulate. This is a natural and non domain-specific physical problem.

Create SysML Model

Component

Discussion

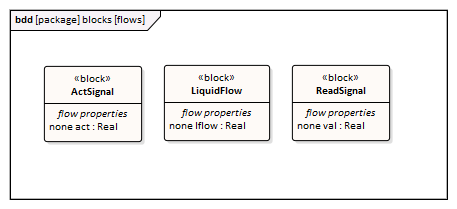
Port Types

The tank has four ports; they are typed to these three blocks:

  • ReadSignal - Reading the fluid level; this has a property 'val' with unit 'm'
  • ActSignal - The signal to the actuator for setting valve position
  • LiquidFlow - The liquid flow at inlets or outlets; this has a property 'lflow' with unit 'm3/s"

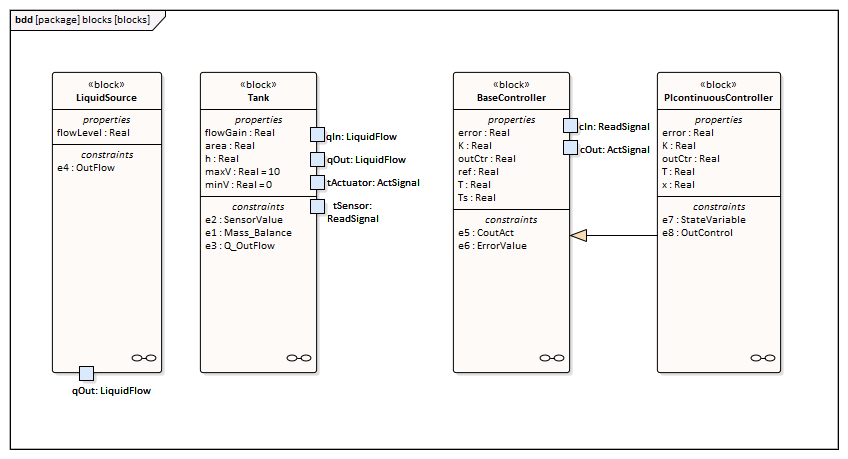
Block Definition Diagram

LiquidSource - The water entering the tank must come from somewhere, therefore we have a liquid source component in the tank system, with the property flowLevel having a unit of 'm3/s'. A Port 'qOut' is typed to 'LiquidFlow'.

Tank - The tanks are connected to controllers and liquid sources through Ports.

  • Each Tank has four Ports:
         -  qIn: for input flow
         -  qOut: for output flow
         -  tSensor: for providing fluid level measurements
         -  tActuator: for setting the position of the valve at the outlet of
            the tank
  • Properties:
         -  area (unit='m2'): area of the tank, involved in the mass balance
               equation
         -  h (unit = 'm'): water level, involved in the mass balance
            equation; its value is read by the sensor
         -  flowGain (unit = 'm2/s'): the output flow is related to the valve
            position by flowGain
         -  minV, maxV: Limits for output valve flow

BaseController - This Block could be super of a PI Continuous Controller and PI Discrete Controller.

  • Ports:
         -  cIn: Input sensor level
         -  cOut: Control to actuator
  • Properties:
         -  Ts (unit = 's'): Time period between discrete samples (not used
             in this example)
         -  K: Gain factor
         -  T (unit = 's'): Time constant of controller
         -  ref: reference level
         -  error: difference between the reference level and the actual
            level of water, obtained from the sensor
         -  outCtr: control signal to the actuator for controlling the valve
            position

PIcontinuousController - generalize from BaseController

  • Properties:
         -  x: the controller state variable

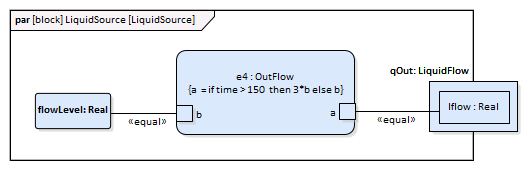
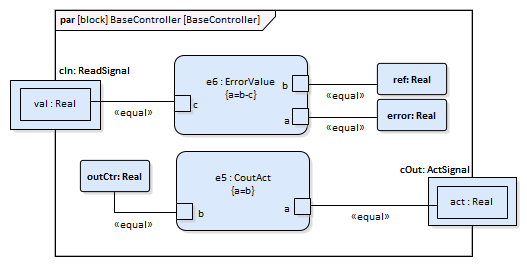
Constraint Blocks

The flow increases sharply at time=150 to a factor of three of the previous flow level, which creates an interesting control problem that the controller of the tank has to handle.

The central equation regulating the behavior of the tank is the mass balance equation.

The output flow is related to the valve position by a 'flowGain' parameter.

The sensor simply reads the level of the tank.

The Constraints defined for 'BaseController' and 'PIcontinuousController' are illustrated in these figures.

Internal Block Diagram

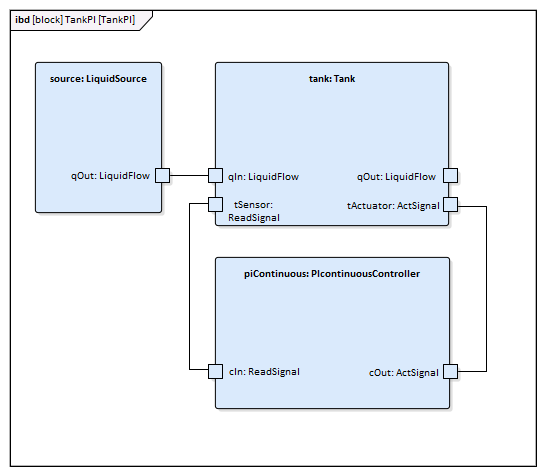
This is the Internal Block diagram for a system with a single tank.

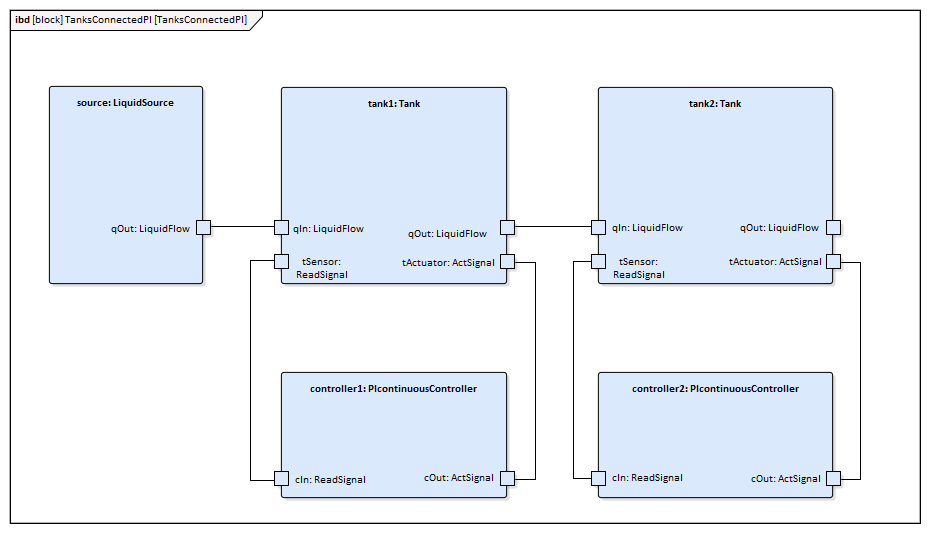
This is the Internal Block diagram for a system with two connected tanks.

Run Simulation

Since TankPI and TanksConnectedPI are defined as 'SysMLSimModel', they will be filled in the combo box of 'Model' on the 'Simulation' page.

Select TanksConnectedPI, and observe these GUI changes happening:

  • 'Data Set' combobox: will be filled with all the data sets defined in TanksConnectedPI
  • 'Dependencies' list: will automatically collect all the Blocks, Constraints, SimFunctions and ValueTypes directly or indirectly referenced by TanksConnectedPI (these elements will be generated as Modelica code)
  • 'Properties to Plot': a long list of 'leaf' variable properties (that is, they don't have properties) will be collected; you can choose one or multiple to simulate, and they will become legends of the plot

Create Artifact and Configure

Select 'Simulate > SysMLSim > Manage > SysMLSim Configuration Manager'

The elements in the Package will be loaded into the Configuration Manager.

Configure these Blocks and their properties as shown in this table.

Note: Properties not configured as 'SimConstant' are 'SimVariable' by default.

Block

Properties

LiquidSource

Configure as 'SysMLSimClass'.

Properties configuration:

  • flowLevel: set as 'SimConstant'

Tank

Configure as 'SysMLSimClass'.

Properties configuration:

  • area: set as 'SimConstant'
  • flowGain: set as 'SimConstant'
  • maxV: set as 'SimConstant'
  • minV: set as 'SimConstant'

BaseController

Configure as 'SysMLSimClass'.

Properties configuration:

  • K: set as 'SimConstant'
  • T: set as 'SimConstant'
  • Ts: set as 'SimConstant'
  • ref: set as 'SimConstant'

PIcontinuousController

Configure as 'SysMLSimClass'.

TankPI

Configure as 'SysMLSimModel'.

TanksConnectedPI

Configure as 'SysMLSimModel'.

Setup DataSet

Right-click on each element, select the 'Create Simulation Dataset' option, and configure the datasets as shown in this table.

Element

Dataset

LiquidSource

flowLevel: 0.02

Tank

h.start: 0

flowGain: 0.05

area: 0.5

maxV: 10

minV: 0

BaseController

T: 10

K: 2

Ts: 0.1

PIcontinuousController

No configuration needed.

By default, the specific block will use the configured values from super block's default dataSet.

TankPI

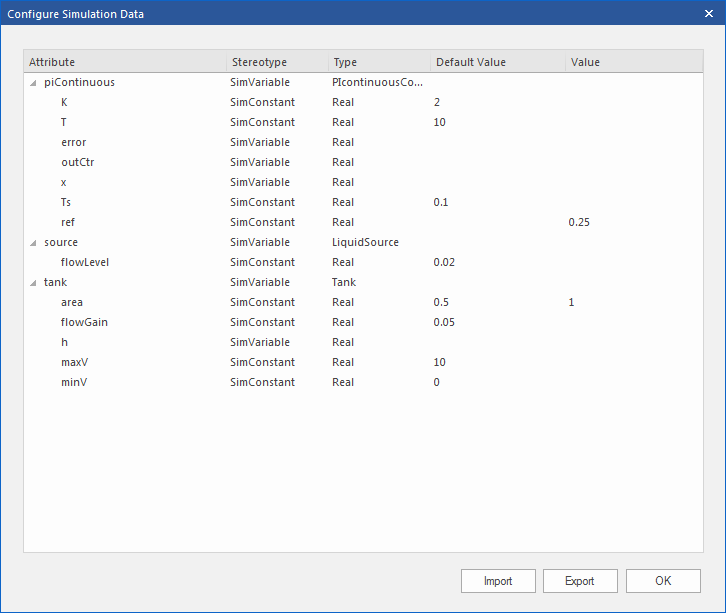
What is interesting here is that the default value could be loaded in the 'Configure Simulation Data' dialog. For example, the values we configured as the default dataSet on each Block element were loaded as default values for the properties of TankPI. Click the icon on each row to expand the property's internal structures to arbitrary depth.

Click on the OK button and return to the Configuration Manager. Then these values are configured:

  • tank.area: 1  this overrides the default value 0.5 defined in the Tank Block's data set
  • piContinuous.ref: 0.25

TanksConnectedPI

  • controller1.ref: 0.25
  • controller2.ref: 0.4

Simulation and Analysis 1

Select these variables and click on the Solve button. This plot should prompt:

  • source.qOut.lflow
  • tank1.qOut.lflow
  • tank1.h
  • tank2.h

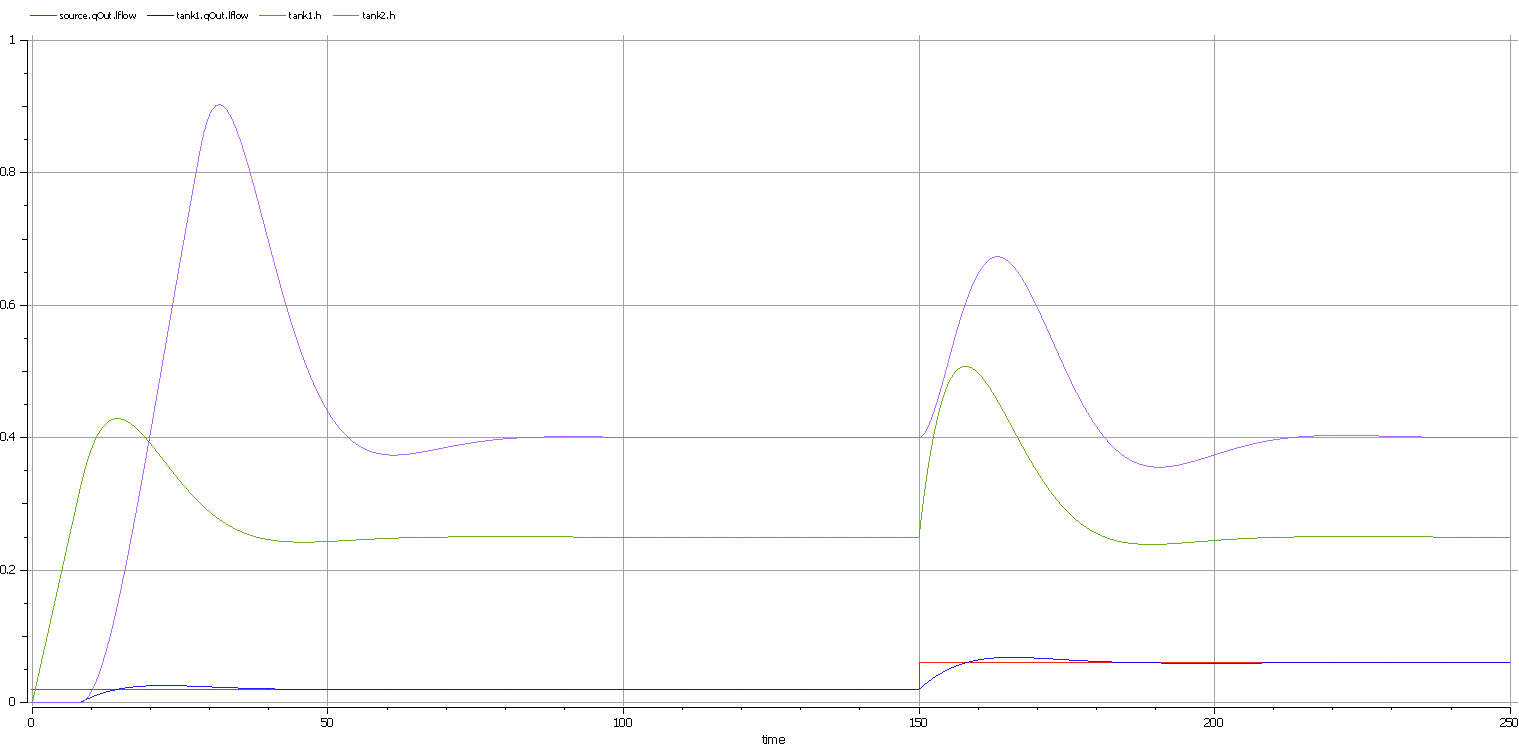
Here are the analyses of the result:

  • The liquid flow increases sharply at time=150, to 0.06 m3/s, a factor of three of the previous flow level (0.02 m3/s)
  • Tank1 regulated at height 0.25 and tank2 regulated at height 0.4 as expected (we set the parameter value through the data set)
  • Both tank1 and tank2 regulated twice during the simulation; the first time regulated with the flow level 0.02 m3/s; the second time regulated with the flow level 0.06 m3/s
  • Tank2 was empty before flow came out from tank1

Simulation and Analysis 2

We have set the tank's properties 'minV' and 'maxV' to values 0 and 10, respectively, in the example.

In the real world, a flow speed of 10 m3/s would require a very big valve to be installed on the tank.

What would happen if we changed the value of 'maxV' to 0.05 m3/s ?

Based on the previous model, we might make these changes:

  • On the existing 'DataSet_1' of TanksConnectedPI, right-click and select 'Duplicate DataSet', and re-name to 'Tank2WithLimitValveSize'
  • Click on the button to configure, expand 'tank2' and type '0.05' in the 'Value' column for the property 'maxV'
  • Select 'Tank2WithLimitValveSize' on the 'Simulation' page and plot for the properties
  • Click on the Solve button to execute the simulation

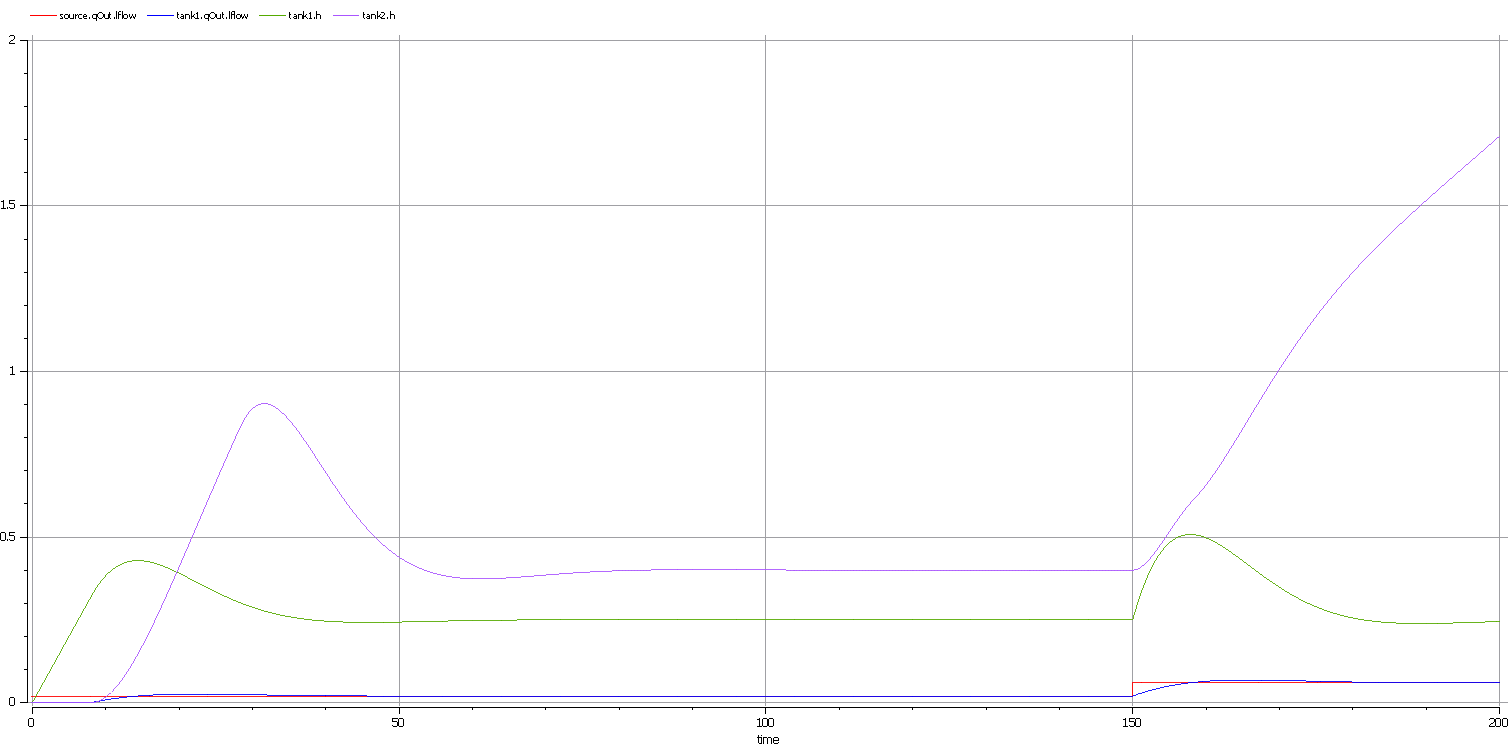
Here are the analyses of the result:

  • Our change only applies to tank2; tank1 can regulate as before on 0.02 m3/s and 0.06 m3/s
  • When the source flow is 0.02 m3/s, tank2 can regulate as before
  • However, when the source flow increases to 0.06 m3/s, the valve is too small to let the out flow match the in flow; the only result is that the water level of tank2 increases
  • It is then up to the user to fix this problem; for example, change to a larger valve, reduce the source flow or make an extra valve

In summary, this example shows how to tune the parameter values by duplicating an existing DataSet.