| Prev | Next |
Mass-Spring-Damper Oscillator Simulation Example
In this section, we will walk through the creation of a SysML parametric model for a simple Oscillator composed of a mass, a spring and a damper, and then use a parametric simulation to predict and chart the behavior of this mechanical system. Finally, we perform what-if analysis by comparing two oscillators provided with different parameter values through data sets.
System being modeled
A mass is hanging on a spring and damper. The first state shown here represents the initial point at time=0, just when the mass is released. The second state represents the final point when the body is at rest and the spring forces are in equilibrium with gravity.

Create SysML Model
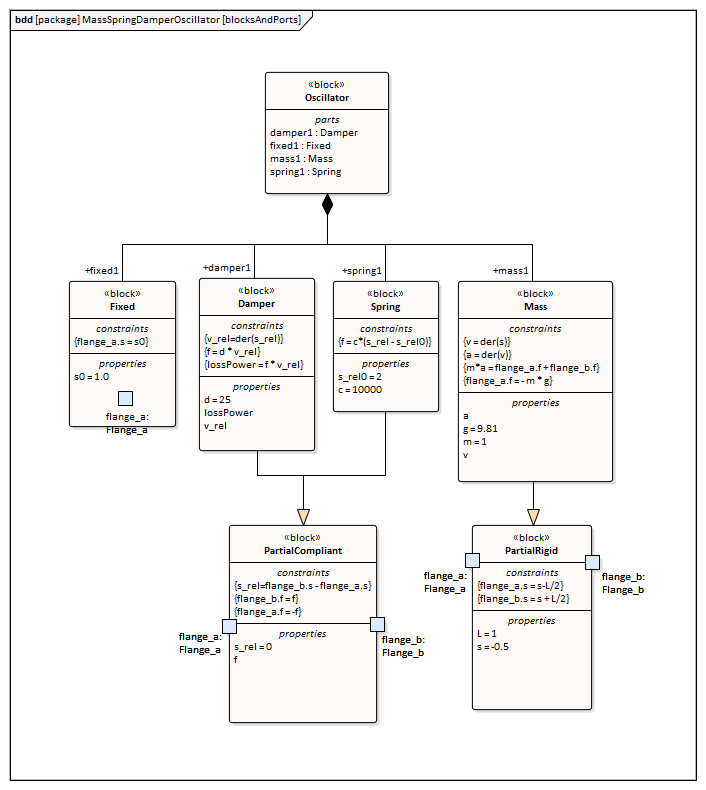
The MassSpringDamperOscillator model in SysML has a main Block, the Oscillator. The Oscillator has four parts: a fixed ceiling, a spring, a damper and a mass body. Create a Block for each of these parts. The four parts of the Oscillator Block are connected through Ports, which represent mechanical flanges.
Components |
Description |
|---|---|
|
Port Types |
The Blocks 'Flange_a' and 'Flange_b' used for flanges in the 1D translational mechanical domain are identical but have slightly different roles, somewhat analogous to the roles of PositivePin and NegativePin in the electrical domain. Momentum is transmitted through the flanges. So the attribute isConserved of flow property Flange.f should be set to True.
|
|
Blocks and Ports |
|
|
Internal structure |
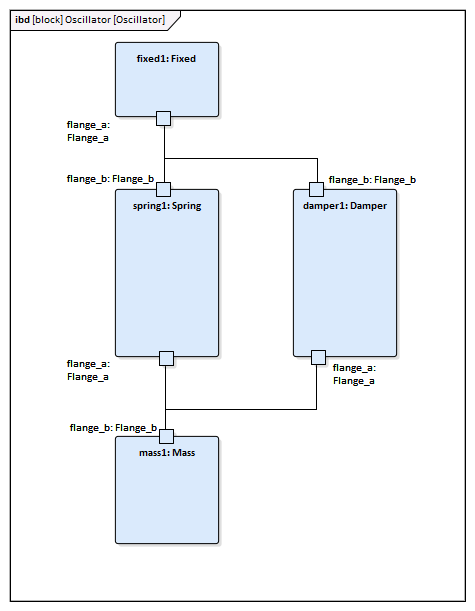
Create an Internal Block diagram (IBD) for 'Oscillator'. Add properties for the fixed ceiling, spring, damper and mass body, typed by the corresponding Blocks. Connect the Ports with connectors.
|
|
Constraints |
For simplicity, we define the constraints directly in the Block elements; optionally you can define Constraint Blocks, use constraint properties in the Blocks, and bind their parameters to the Block's properties. |
Two Oscillator Compare Plan
After we model the Oscillator, we want to do some what-if analysis. For example:
- What is the difference between two oscillators with different dampers?
- What if there is no damper?
- What is the difference between two oscillators with different springs?
- What is the difference between two oscillators with different masses?
Here are the steps for creating a comparison model:
- Create a Block named 'OscillatorCompareModel'
- Create two Properties for 'OscillatorCompareModel', called oscillator1 and oscillator2, and type them with the Block Oscillator

Setup DataSet and Run Simulation
Create a SysMLSim Configuration Artifact and assign it to this Package. Then create these data sets:
- Damper: small VS big
provide 'oscillator1.damper1.d' with the value 10 and 'oscillator2.damper1.d' with the larger value 20
- Damper: no vs yes
provide 'oscillator1.damper1.d with the value 0; ('oscillator2.damper1.d' will use the default value 25)
- Spring: small vs big
provide 'oscillator1.spring1.c' with the value 6000 and 'oscillator2.spring1.c' with the larger value 12000
- Mass: light vs heavy
provide 'oscillator1.mass1.m' with the value 0.5 and 'oscillator2.mass1.m' with the larger value 2
The configured page resembles this:

On the 'Simulation' page, select 'OscillatorCompareModel', plot for 'oscillator1.mass1.s' and 'oscillator2.mass1.s', then choose one of the created datasets and run the simulation.
Tip: If there are too many properties in the plot list, you can toggle the bar using the context menu on the list header, then type in 'mass1.s' in this example.

These are the simulation results:
- Damper, small vs big: the smaller damper makes the body oscillate more

- Damper, no vs yes: the oscillator never stops without a damper

- Spring, small vs big: the spring with smaller 'c' will oscillate more slowly

- Mass, light vs heavy: the object with smaller mass will oscillate faster and regulate quicker